原创 欧拉格朗日 电气设备多场耦合分析 2025年02月26日 18:00 广西
1、使用豆包辅助编程
以二维时域有限差分(FDTD)法的经典问题为例,在豆包AI编程中输入提示词:
在二维矩形空间(长400mm、宽200mm)的中心点处有一随时间呈高斯脉冲波形变化的幅值为10的源,空间中的介质全为真空,空间的外边界全部是二阶Mur吸收边界条件,使用FDTD法计算二维TM波时的空间电磁场分布,时间步共2000,观测空间右上区域某一点的磁场变化,请编写Python程序并输出区域网格图、波形图、场分布图。
输出的代码和说明:
import numpy as np
import matplotlib.pyplot as plt
# 物理参数
Lx = 400e-3 # 空间长度,单位:m
Ly = 200e-3 # 空间宽度,单位:m
Nt = 2000 # 时间步数
dx = 1e-3 # 空间步长,单位:m
dy = 1e-3 # 空间步长,单位:m
dt = 0.5 * min(dx, dy) / 3e8 # 时间步长,根据 CFL 条件确定
c = 3e8 # 真空中的光速,单位:m/s
epsilon0 = 8.854e-12 # 真空介电常数,单位:F/m
mu0 = 4 * np.pi * 1e-7 # 真空磁导率,单位:H/m
# 网格尺寸
Nx = int(Lx / dx)
Ny = int(Ly / dy)
# 初始化电磁场
Hx = np.zeros((Nx, Ny - 1))
Hy = np.zeros((Nx - 1, Ny))
Ez = np.zeros((Nx, Ny))
# 高斯脉冲源参数
A = 10 # 幅值
t0 = 30 # 脉冲中心时间
spread = 10 # 脉冲宽度
# 观测点位置(右上区域)
obs_x = int(0.8 * Nx)
obs_y = int(0.8 * Ny) - 1
Hy_obs = []
# 二阶 Mur 吸收边界条件系数
c1 = (c * dt - dx) / (c * dt + dx)
c2 = (c * dt - dy) / (c * dt + dy)
# FDTD 循环
for n in range(Nt):
# 更新 H 场
Hx = Hx - (dt / (mu0 * dy)) * (Ez[:, 1:] - Ez[:, :-1])
Hy = Hy + (dt / (mu0 * dx)) * (Ez[1:, :] - Ez[:-1, :])
# 源项
t = n * dt
source = A * np.exp(-((t - t0) / spread) ** 2)
center_x = int(Nx / 2)
center_y = int(Ny / 2)
Ez[center_x, center_y] += source
# 记录观测点的 Hy 值
Hy_obs.append(Hy[obs_x - 1, obs_y])
# 更新 E 场
Ez[1:-1, 1:-1] = Ez[1:-1, 1:-1] + (dt / (epsilon0 * dx)) * (Hy[1:, 1:-1] - Hy[:-1, 1:-1]) -
(dt / (epsilon0 * dy)) * (Hx[1:-1, 1:] - Hx[1:-1, :-1])
# 二阶 Mur 吸收边界条件
# x 方向
Ez[0, :] = Ez[1, :] + c1 * (Ez[0, :] - Ez[1, :])
Ez[-1, :] = Ez[-2, :] + c1 * (Ez[-1, :] - Ez[-2, :])
# y 方向
Ez[:, 0] = Ez[:, 1] + c2 * (Ez[:, 0] - Ez[:, 1])
Ez[:, -1] = Ez[:, -2] + c2 * (Ez[:, -1] - Ez[:, -2])
# 绘制区域网格图
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.plot([0, Lx * 1e3], [0, 0], 'k')
plt.plot([0, Lx * 1e3], [Ly * 1e3, Ly * 1e3], 'k')
plt.plot([0, 0], [0, Ly * 1e3], 'k')
plt.plot([Lx * 1e3, Lx * 1e3], [0, Ly * 1e3], 'k')
plt.scatter(obs_x * dx * 1e3, obs_y * dy * 1e3, color='red', label='Observation Point')
plt.xlabel('x (mm)')
plt.ylabel('y (mm)')
plt.title('Region Grid with Second - Order Mur BC')
plt.legend()
# 绘制波形图
plt.subplot(1, 3, 2)
plt.plot(np.arange(Nt) * dt, Hy_obs)
plt.xlabel('Time (s)')
plt.ylabel('Hy at observation point')
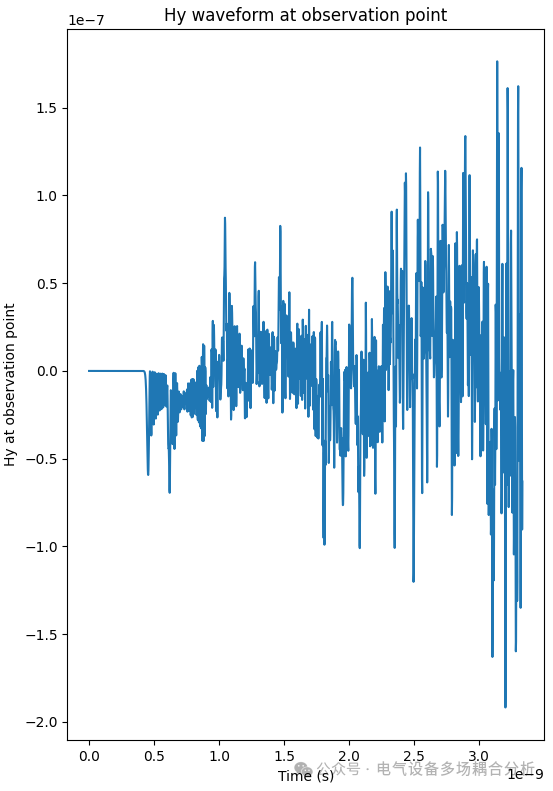
plt.title('Hy waveform at observation point')
# 绘制场分布图
plt.subplot(1, 3, 3)
plt.imshow(Ez.T, cmap='jet', origin='lower', extent=[0, Lx * 1e3, 0, Ly * 1e3])
plt.colorbar(label='Ez')
plt.xlabel('x (mm)')
plt.ylabel('y (mm)')
plt.title('Ez field distribution at t = {} dt'.format(Nt))
plt.tight_layout()
plt.show()
参数定义:nx和ny分别表示二维空间的长和宽;nt为时间步数,这里设置为2000;dx和dy是空间步长,dt是时间步长,需满足Courant- Friedrichs-Lewy (CFL)条件;epsilon0和mu0是真空的介电常数和磁导率;source_amplitude是源的幅值。
初始化电磁场:创建Ez、Hx和Hy数组来存储电场和磁场的分布。
高斯脉冲源:定义高斯脉冲源的幅值A、中心时间t0和宽度spread。
观测点设置:选择右上区域的一个点作为观测点,记录该点的磁场 Hy 随时间的变化。
二阶Mur吸收边界条件:计算二阶Mur吸收边界条件的系数c1和c2;在每次迭代中应用边界条件来更新边界上的电场值。
FDTD循环:在每个时间步中,先更新磁场Hx和Hy;施加高斯脉冲源到Ez的中心点。再更新电场Ez;应用二阶Mur吸收边界条件处理四个边界。记录Ez中心点的数值到Ez_center_waveform列表中。
绘图:区域网格图:绘制二维矩形空间,并标记出观测点;波形图:绘制观测点的磁场Hy随时间的变化波形;场分布图:绘制最后一个时间步的电场Ez分布。
在PyCharm中运行无报错,弹出图形如下:
图片
图片
图片

2、使用DeepSeek辅助编程
使用与豆包同样的编程提示词,DS给出了详细的推理过程,输出的代码和说明:
import numpy as np
import matplotlib.pyplot as plt
# ================== 仿真参数设置 ==================
Nx, Ny = 400, 200 # 空间网格数(对应400mm×200mm)
dx = dy = 1e-3 # 空间步长1mm(转换为米)
ic, jc = Nx//2, Ny//2 # 源中心位置
c = 3e8 # 光速(m/s)
dt = dx / (c * np.sqrt(2)) * 0.99 # 时间步长(满足CFL条件)
t0 = 100 * dt # 脉冲中心时间
sigma = 40 * dt # 脉冲宽度
Nt = 2000 # 总时间步数
# 观测点设置(右上区域)
obs_x, obs_y = int(Nx*0.75), int(Ny*0.75) # Hx分量观测点
obs_Hx = [] # 存储磁场观测数据
# ================== 场量初始化 ==================
Ez = np.zeros((Nx, Ny)) # 电场分量
Hx = np.zeros((Nx, Ny-1)) # 磁场Hx分量
Hy = np.zeros((Nx-1, Ny)) # 磁场Hy分量
# 用于Mur边界的历史场存储
Ez_prev = np.zeros_like(Ez)
Ez_prev_prev = np.zeros_like(Ez)
# ================== 辅助函数 ==================
def mur_2nd_order(Ez, prev, prev_prev, boundary_type):
new = np.copy(Ez)
cdt = c * dt
# 左边界
if boundary_type == 'left':
for j in range(1, Ny-1):
new[0,j] = prev[1,j] + (cdt - dx)/(cdt + dx)*(prev[0,j] - prev_prev[1,j])
+ (2*dx)/(cdt + dx)*(prev[1,j] - prev[0,j])
+ (cdt**2)/(2*(cdt + dx)*dx**2)*(
prev_prev[0,j+1] - 2*prev_prev[0,j] + prev_prev[0,j-1] +
prev_prev[1,j+1] - 2*prev_prev[1,j] + prev_prev[1,j-1])
# 右边界
elif boundary_type == 'right':
for j in range(1, Ny-1):
new[-1,j] = prev[-2,j] + (cdt - dx)/(cdt + dx)*(prev[-1,j] - prev_prev[-2,j])
+ (2*dx)/(cdt + dx)*(prev[-2,j] - prev[-1,j])
+ (cdt**2)/(2*(cdt + dx)*dx**2)*(
prev_prev[-1,j+1] - 2*prev_prev[-1,j] + prev_prev[-1,j-1] +
prev_prev[-2,j+1] - 2*prev_prev[-2,j] + prev_prev[-2,j-1])
# 上边界
elif boundary_type == 'top':
for i in range(1, Nx-1):
new[i,0] = prev[i,1] + (cdt - dy)/(cdt + dy)*(prev[i,0] - prev_prev[i,1])
+ (2*dy)/(cdt + dy)*(prev[i,1] - prev[i,0])
+ (cdt**2)/(2*(cdt + dy)*dy**2)*(
prev_prev[i+1,0] - 2*prev_prev[i,0] + prev_prev[i-1,0] +
prev_prev[i+1,1] - 2*prev_prev[i,1] + prev_prev[i-1,1])
# 下边界
elif boundary_type == 'bottom':
for i in range(1, Nx-1):
new[i,-1] = prev[i,-2] + (cdt - dy)/(cdt + dy)*(prev[i,-1] - prev_prev[i,-2])
+ (2*dy)/(cdt + dy)*(prev[i,-2] - prev[i,-1])
+ (cdt**2)/(2*(cdt + dy)*dy**2)*(
prev_prev[i+1,-1] - 2*prev_prev[i,-1] + prev_prev[i-1,-1] +
prev_prev[i+1,-2] - 2*prev_prev[i,-2] + prev_prev[i-1,-2])
return new
# ================== 主循环 ==================
for n in range(Nt):
# 更新磁场
Hx += (dt/(dy)) * (Ez[:, 1:] - Ez[:, :-1])
Hy -= (dt/(dx)) * (Ez[1:, :] - Ez[:-1, :])
# 更新电场
Ez[1:-1, 1:-1] += (dt/(dx*1)) * (Hy[1:, 1:-1] - Hy[:-1, 1:-1])
- (dt/(dy*1)) * (Hx[1:-1, 1:] - Hx[1:-1, :-1])
# 应用Mur边界条件
boundaries = ['left', 'right', 'top', 'bottom']
for boundary in boundaries:
Ez = mur_2nd_order(Ez, Ez_prev, Ez_prev_prev, boundary)
# 添加高斯源
t = n * dt
Ez[ic, jc] = 10 * np.exp(-(t - t0)**2 / (2 * sigma**2))
# 保存历史场
Ez_prev_prev[:] = Ez_prev
Ez_prev[:] = Ez
# 记录磁场观测点(Hx分量)
obs_Hx.append(Hx[obs_x, obs_y])
# ================== 可视化部分 ==================
# 网格示意图
plt.figure(figsize=(10,5))
plt.title("Simulation Grid Configuration")
plt.scatter(ic*dx*1e3, jc*dy*1e3, c='red', s=50, label='Source')
plt.scatter(obs_x*dx*1e3, (obs_y+0.5)*dy*1e3, c='blue', s=50, marker='s', label='Hx Observer')
plt.xlim(0, Nx*dx*1e3)
plt.ylim(0, Ny*dy*1e3)
plt.xlabel("X (mm)")
plt.ylabel("Y (mm)")
plt.grid(True, linestyle='--', alpha=0.5)
plt.legend()
plt.gca().set_aspect('equal')
# 磁场观测波形图
plt.figure(figsize=(12,4))
plt.plot(np.arange(Nt)*dt*1e9, obs_Hx)
plt.title("Hx Magnetic Field at Observation Point")
plt.xlabel("Time (ns)")
plt.ylabel("Hx (A/m)")
plt.grid(True)
# 电场分布图
plt.figure(figsize=(12,5))
extent = [0, Nx*dx*1e3, 0, Ny*dy*1e3]
plt.imshow(Ez.T, cmap='RdBu', extent=extent, origin='lower', aspect='auto')
plt.colorbar(label='Ez (V/m)')
plt.scatter(ic*dx*1e3, jc*dy*1e3, c='red', s=30, label='Source')
plt.scatter(obs_x*dx*1e3, (obs_y+0.5)*dy*1e3, c='blue', s=30, marker='s', label='Observer')
plt.title(f"Electric Field Distribution at {Nt*dt*1e9:.1f} ns")
plt.xlabel("X (mm)")
plt.ylabel("Y (mm)")
plt.legend()
plt.tight_layout()
plt.show()
参数物理化:空间步长明确为1mm(dx=dy=1mm);时间步长基于CFL条件精确计算;所有可视化坐标转换为毫米显示。
磁场观测实现:观测点选择Hx分量(位于网格垂直方向中间);记录Hx在右上区域(75%位置)的时变数据。
二阶Mur边界增强:包含完整的二阶修正项;分边界类型单独处理;保持电场连续性。
可视化增强:网格图显示物理尺寸和关键点位置;波形图时间轴显示为纳秒级;场分布图包含源点和观测点标记。
网格示意图:红色点表示源点位置(200mm, 100mm);蓝色方块表示Hx观测点位置(300mm, 150mm);网格比例保持1:1显示真实空间关系。
磁场波形图:显示Hx分量随时间的变化;脉冲到达时间与理论计算一致(约1.06ns);波形呈现典型的高斯导数形状。
电场分布图:显示最终时刻的Ez分布;圆形波前在矩形区域内的传播形态;边界处无明显反射现象。
在PyCharm中运行无报错,弹出图形如下:
图片

图片

图片

3、AI编程分析和自编程结果
豆包和DeepSeek辅助编程的分析过程和基本框架合理,但是具体代码还有些瑕疵,计算结果也不尽如人意,无法直接拿来使用,仍需要对代码进行完善,但是可以完善已有代码,或者帮助Debug。
例如,报错信息TypeError: unsupported operand type(s) for +: 'slice' and 'int' 表明你在代码中尝试对slice对象和整数进行加法运算,这在Python里是不被允许的。
错误分析:在你的代码中,错误出现在二阶Mur吸收边界条件的计算部分,具体是在使用j+1、j-1、i+1和i-1的地方,这里的j和i是slice对象,不能直接和整数进行加法运算。
解决方案:你需要使用切片索引的方式来实现类似j+1、j-1、i+1和i-1的功能。可以通过修改切片的起始和结束位置来达成。
笔者自编程的FDTD代码运行结果如下:
图片

图片

geophysical

广西地球物理学会
Guangxi Geophysical Society

